Различные виды интерполяции. Воссоздание высоких частот

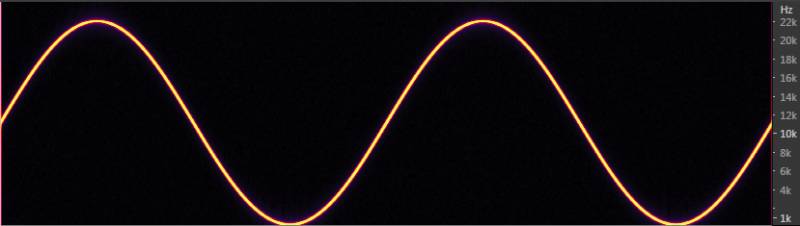
Примечание: сия статья ни в коем случае не является пособием для апконвертщиков (коим в аду специально уготовлено жаркое местечко) и опубликована лишь для общего развития; а также пущего понимания теории цифрового звука.

Виды интерполяции

Как известно, цифровой сигнал представляет собой набор отсчетов (семплов) с разным уровнем, которые следуют один за одним с определенной фиксированной (для привычной нам импульсно-кодовой модуляции) частотой. В определенных случаях частоту следования семплов (частоту дискретизации) может потребоваться изменить, т.е. может потребоваться т.н. ресемплинг. Ресемплинг условно можно разделить на два вида — с повышением частоты (апсемплинг) и понижением (даунсемплинг). И вот тут возникает вопрос: а каким же образом нам изменить количество семплов в потоке? Какие семплы отбросить, или же наоборот — как рассчитать уровень новых, промежуточных семплов?

Давайте для простоты ограничимся апсемплингом. Скажем, пускай нам надо повысить частоту дискретизации в два раза. Для этого надо удвоить количество семплов, т.е в промежутках между семплами вставить один дополнительный.

Рассмотрим вот такой сигнал:

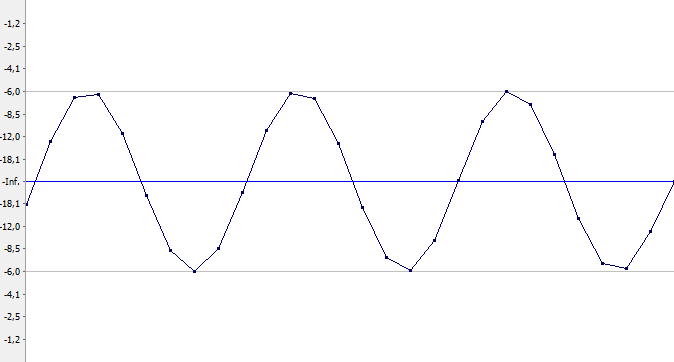
Это три периода синусоидального сигнала с частотой 5000 Гц, оцифрованного с частотой дискретизации 44100 Гц (глубина квантования равна 32 битам, но для нас это не важно). Фактически смысл здесь имеют лишь точки (это и есть те самые семплы), линии между ними рисует программа Sound Forge. Как видим, на один период приходится примерно 9 семплов (441000/5000≈9). Нам надо увеличить это количество вдвое. Где же именно нам разместить промежуточные семплы?

Есть несколько способов расчета уровня промежуточных семплов (то есть интерполяции). Как я уже сказал, программа сама дорисовала линии, соединяющие соседние семплы. Эти линии — прямые, и если мы разместим промежуточный семпл (или семплы, если увеличиваем частоту более, чем в два раза) на этой линии, такой вид интерполяции будет называться линейной. Расчетную формулу для получения уровня промежуточного семпла можно найти из уравнения прямой. Уровень семпла x, находящегося между семплами x0 и x1 будет равен:

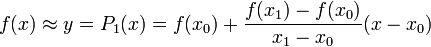
Результат преобразования частоты в 88.2 кГц будет следующим:

Собственно, отличий между двумя волнами вы не найдете, кроме количества семплов на период конечно.

Теперь давайте возьмем сигнал с плавающей частотой (частота дискретизации 48 кГц) и сравним спектрограммы исходного и полученного после увеличения частоты дискретизации в два раза:

Мы видим, что в сигнале появились новые частотные составляющие: исходный спектр буквально отразился в высокочастотную область. Это явление называется алиазингом (alias — отражение). Кстати, надо отметить, что с понижением частоты сигнала уровень алиаса уменьшается. Это связано с уменьшением погрешности линейной интерполяции: при уменьшении разницы между уровнями соседних семплов (т.е. при уменьшении скорости нарастания сигнала, которая прямо пропорциональна частоте), ошибка квантования стремится к нулю.

Но есть еще более простой способ интерполяции, называемый интерполяцией нулевого порядка. Он даже не требует никаких расчетов: дополнительный семпл по уровню соответствует предыдущему.

Да, это те самые ступеньки, в виде которых непросвещенные люди так любят изображать цифровой сигнал. В случае со свип сигналом (плавающая частота) мы получим такую картинку:

Теперь мы получили точную копию исходного сигнала в области расширенного диапазона (отражение идет симметрично относительно исходной частоты Найквиста).

Надо отметить, что подобная картинка получается исключительно при кратном повышении частоты дискретизации (2x, 3x, 4x и т.д.). При дробном множителе мы получим сильные искажения во всем спектре частот.

Этот метод интерполяции активно используется в ЦАП (сигма-дельта ЦАП использует многократный ампсемплинг) — да, на определенном этапе оцифрованный сигнал действительно представляется в виде ступенек. Однако, после преобразования применяется фильтр низких частот, который фактически сглаживает сигнал.

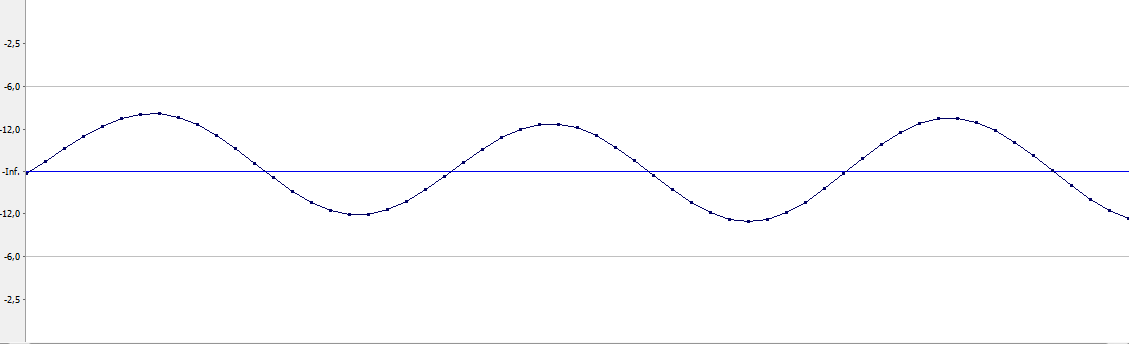
На рисунке вы видите результирующий сигнал, полученный после фильтрации предыдущего, ступенчатого сигнала. Мы видим, что результирующая интерполяция получилась даже лучше линейной. Причиной этому является отсутствие дополнительных частотных составляющих, которые мы вырезали НЧ фильтром. Кстати говоря, убедиться, что в результате ЦА преобразования также не получается никаких ступенек, вы можете посмотрев это видео.

Именно так работают почти все ресемплеры: сначала количество семплов добивается до нужного путем копирования предыдущих, а затем полученный сигнал фильтруется примерно до исходной частоты Найквиста (чтобы отбросить отражение, т.е. алиазинг).

В зависимости от типа используемого НЧ фильтра и различают алгоритмы передискретизации. Наиболее популярным является sinc интерполяция с использованием sinc фильтра.

Более подробно о передискретизации можно почитать в статье Конвертеры частоты дискретизации. Мы же перейдем к одному интересному применению интерполяции нулевого порядка.

Воссоздание высоких частот

Для данного опыта нам понадобятся: foobar2000, ресемплеры, SSRC X, SoX, Secret Rabbit Code, а также SoX Lowpass filter. Всё это можно скачать на странице foobar2000 + плагины.

В качестве подопытного возьмем семпл из трека «Armin van Buuren — Sail». Семпл имеет широкий частотный диапазон:

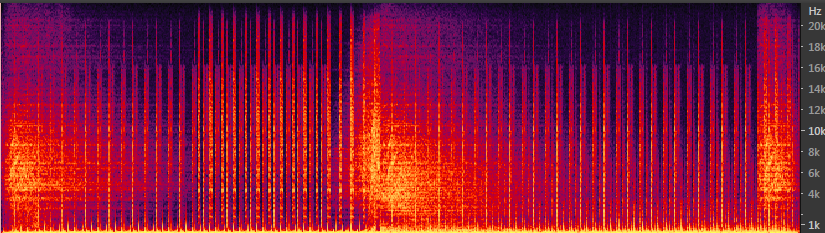
Теперь урежем частотный диапазон с помощью DSP Lowpass (SoX) до 12.5 кГц. Вот спектр результирующего семпла:

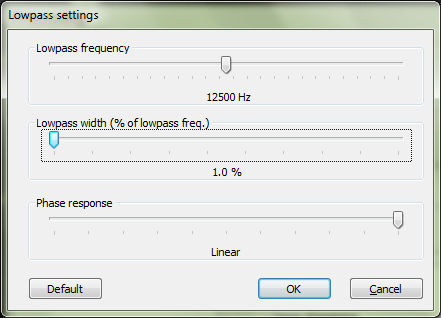
Ну, проблему создали, теперь самое время её решать.

Фишка интерполяции нулевого порядка как раз в том, что она умеет отражать более низкие частоты в область более высоких. Таким образом мы можем восстановить некое подобие высоких частот, которые по уровню будут зависеть от более низких. Для этого надо выполнить следующее:

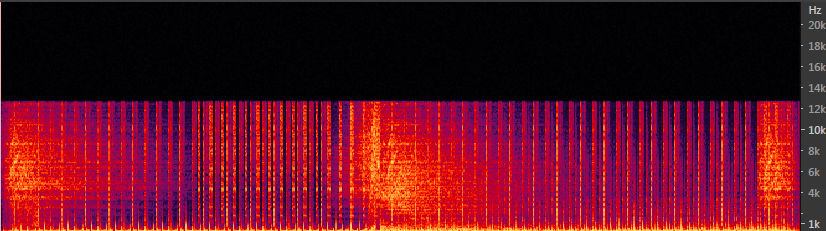
1. Определить частоту среза. В нашем случае это 12.5 кГц.
2. Выполнить ресемплирование до частоты приблизительно в два (но не более!) раза больше частоты среза. В данном случае нам идеально подойдет частота 24 кГц. Для ресемплирования воспользуемся SSRC X с максимальной полосой пропускания, которую обеспечивает пресет Otachan Ultra:

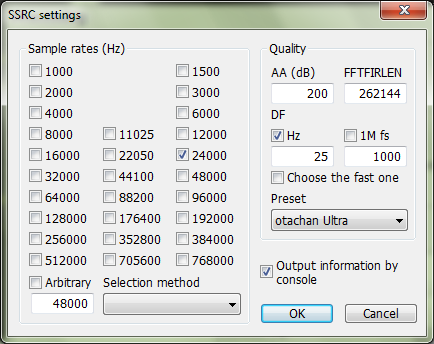
Это будет первое звено в цепочке DSP.

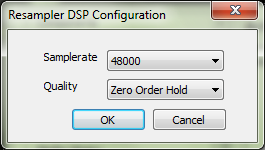
4. Выполнить ресемплирование до нужной частоты дискретизации. Это необходимо, например, если мы восстанавливали диапазон 8-16 кГц и результирующая частота дискретизации вышла 32 кГц, в то время как нам может понадобиться 44.1. Ресемплирования следует производить с помощью SoX Resampler. В нашем случае частота 48 кГц вполне приемлема.

Вот, собственно, и всё. На выходе мы получаем сигнал с полным спектром:

В принципе, можно использовать и линейную интерполяцию. Тогда мы получим более естественную спектрограмму со спадом в области ВЧ:

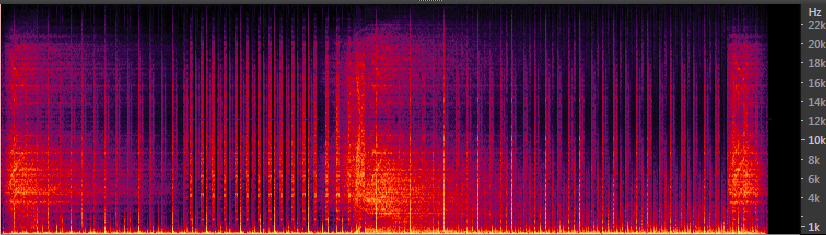
Таким же образом можно воссоздать ВЧ при срезе на 16-17 кГц. Для этого выполняется даунсемплинг до 32 кГц, затем частота повышается с помощью интерполяции нулевого порядка (или линейной) до 64 кГц, после чего производится ресемплирование с помощью SoX до 44.1 кГц.

Впрочем, всё это извращение, и по-хорошему подходит разве что для забавы. Тем не менее, если сравнить семпла со срезом на 12.5 кГц и семпл полученный после воссоздания высоких частот, можно согласиться, что второй субъективно звучит лучше.

На этом всё. Надеюсь, вам было интересно. Удачи!